Chapter 2 Methodology
This chapter describes the methodology of the model, providing sample data tables throughout to demonstrate how various decisions were made and how pieces of the model are specified.
2.1 Overview
The model was developed to simulate the range of outcomes likely for a given set of inputs. In statistical terminology, this is called a Bayesian model, where instead of assuming a single value for a particular parameter in a model – in this model there are a variety of such parameters – we use a probabilistic distribution (e.g., the normal distribution) generated from observed data to draw random values from that distribution where each parameter is used in the model. To make this style of model useful, we run the simulation hundreds (or thousands, depending on the number of different parameters and the range of their respective distributions) of times to generate a range of potential outcomes. This range of outcomes is its own statistical distribution, with sample statistics (e.g. mean, median) that can be used to represent the distribution at a summary level.
This style of model was chosen because there are many parameters in this modeling exercise that belong to distributions that can wary widely from day to day, and simply assuming a single value at each of these points in the simulation constrains the model to a relatively narrow set of possible outcomes. With this Bayesian model, we are more confident that the range of likely outcomes is represented by the results, so that both the typical high/low scenarios can be prepared for, not just the average.
2.2 Key Assumptions
This section documents key simplifying assumptions that were made throughout the modeling process in consultation with Translink staff.
2.2.1 Aggregations
All of these aggregations were discussed in the scoping of this modeling effort, and are documented below for background in future use of the model.
2.2.1.1 TAZ Trip Aggregation
Trip origins and destinations were aggregated to TAZs and modeled based on TAZ to TAZ trip pairs. While this is significantly higher resolution than the previous model, which considered trip OD pairs only at the sub-region to sub-region level, it is still a simplifying assumption to note. Modeling trips at the TAZ OD pair level is typical for travel demand modeling in general.
2.2.1.2 Time Bin Aggregation
Data were aggregated to time bins slightly expanded from the first iteration of the model, mainly to separate out evening trips from overnight trips. The revised time of day bins are the following:
- Early Morning: 5 am to 8 am (3 hours)
- Morning: 8 am to 12 pm (4 hours)
- Early Afternoon: 12 pm to 4 pm (4 hours)
- Late Afternoon/Evening: 4 pm to 10 pm (6 hours)
- Overnight: All other hours (10 pm - 5 am, 7 hours)
2.2.1.3 Day of Week Aggregation
Data were aggregated to weekday and weekend as in the first iteration of the model – demand patterns vary widely between these two groups, but within the groups vary little enough that it is not worth stratifying the model by specific day of week.
2.2.1.4 Month Aggregation
Data were aggregated by month to allow for seasonal differences in demand patterns to be represented by the model. While seasonal differences in demand patterns surely are not fully determined by the month of year, this was a simplifying assumption made in the previous iteration of the model and carried through to this one.
2.2.2 Eligible Garage Assignment
The HandyDART service area is divided to into six subregions, and there is a HandyDART depot located to serve each of them. While the majority of trips originating from a particular subregion are served by that subregion’s depot, not all of the trips are. This is an efficient way to operate, as there are a variety of situations in which a trip might be more efficiently served by a vehicle originating from a different depot; such as when a longer haul trip across subregions can be paired with a trip that sends that vehicle back to its origin subregion, or when trips are on the boundaries of a subregion where one subregion is more service constrained than another. We first wanted to understand the prevalence of this behavior, and so made a map based on the observed data provided.
This map illustrates the probability of a trip originating in a particular Transportation Analysis Zone (TAZ) being served by the selected garage (switch which garage is considered with the layer switcher in the upper right hand corner).
Figure 2.1: Map of Probability of Trip Originating in a TAZ being Served by Selected Garage
Based on the observed data in the above map and in consultation with Translink, it was decided that we would constrain the model to only assigning trips originating in a given to TAZ to either a) that TAZ’s subregion garage, or b) the garage second likeliest to be assigned for that TAZ, based on 2019-2020 observations. Overall, this resulted in 24 different assignment groups. The distribution of how observed trips were assigned to garages is described in the following table. Based on this grouping, we are only simplifying the garage assignment behavior for 2% of observed trips to be constrained to this primary/secondary framework.
Figure 2.2: 2019/2020 Observed Garage Assignment Group Patterns
2.3 Scenario Setup
A total of 32 different scenarios were considered using the model outlined hereien. The 32 scenarios are the product of:
- 3 different social distancing regimes: 6-foot (existing), 3-foot, and 0-foot (no social distancing)
- 15 different ridership return levels (50% - 120% at 5% increments). Some of these social distancing - ridership return matches were not considered (otherwise we would have 3*15=45 different scenarios) because it was assumed they were very unrealistic to begin with (e.g., 120% ridership return at 6-foot social distancing).
Those scenarios are enumerated below for documentation purposes.
Figure 2.3: Scenario Definitions
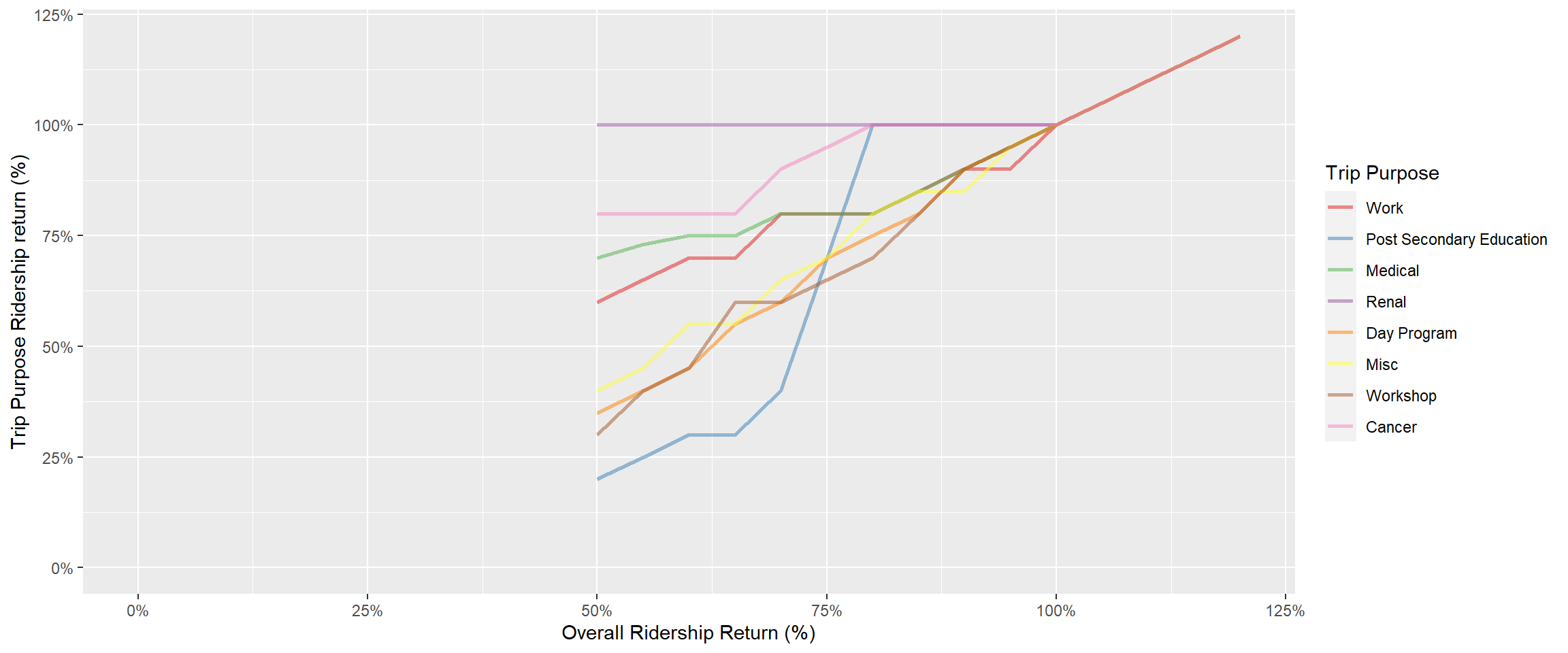
For each of the 15 different ridership return levels, trip purpose level ridership return values were provided by Translink that would provide a reasonable assumption for how the total ridership return rate would be achieved. This was done because different trip purposes have already and will continue to return at different rates. For example, Renal trips already operate at approximately 100% of pre-COVID levels, whereas workshop trips operate at much lower rates. The ridership return rates assumed for the model are tabulated (and illustrated) below for documentation purposes. In a future version of the model, these values could be manipulated.
Figure 2.4: Trip Type Pattern Definitions
Figure 2.5: Trip Type Pattern Illustration
2.4 Model Steps
The following steps are run for each model scenario for as many simulations per scenario are desired to be run. For initial model testing, we only ran 100 simulations, but to generate a robust distribution for the final outputs, we ran each scenario 300 times.
2.4.1 Step 1: Trip Generation
2.4.1.1 Trip Arrivals
For each scenario, the first quantity to be simulated is the trip arrival rate for each TAZ pair (within each trip purpose, time bin, month, and day type) – this is a the parameter used to describe the Poisson distribution, from which random arrival rates (varying similarly to the observed arrival rates) can be selected. The Poisson distribution is used to simulate this behavior for several reasons:
- Visual inspection of the distribution of daily trips generated for sample TAZ pairs showed distributions similar to the shape of the Poisson distribution
- The Poisson distribution naturally generates integer values, which are perfect for understanding trip generation – a fraction of a trip is not generated in the real world.
- Poisson distributions are typically used for modeling transportation arrival processes, or any natural phenomena involving an arrival rate (e.g., call centers use them to forecast calls generated).
A Poisson distribution is described by single parameter – the mean arrival rate. For each TAZ OD pair, trip purpose, time of day bin, day type, and month, a mean arrival rate was calculated from the observed 2019 data. This arrival rate was then multiplied by the ridership return for the given trip purpose and scenario. This modified arrival rate was used to describe the Poisson distribution from which an estimate of the number of forecasted trips (for the OD pair, trip purpose, time of day bin, day type, and month) could be drawn on each simulation.
2.4.1.2 Passengers per Trip
Now that we have generated the trips, we need to figure out how many passengers are part of each trip, and what type of passengers they are (passengers are divided into ambulatory and wheelchair passengers because of their different vehicle capacity needs). A Normal distribution is used here for a similar simulation process. The Normal distribution was chosen for the following reasons:
- Visual inspection of the distribution of passengers per trip generated for sample TAZ pairs showed distributions similar to the shape of the Normal distribution.
- The normal distribution does not have the long right tail of the Poisson distribution. Initially, we tried using the Poisson distribution for this process, but the simulation occasionally returned numbers of passengers much higher than what was observed or would be realistic (especially in COVID-19 conditions). The normal distribution has the benefit of being described by both the mean and the standard deviation, which describes the spread of the data. This enabled estimates to be much more stable.
- A drawback of the normal distribution is it is continuous, producing decimal numbers. After the passenger type proportions (described in a moment) were applied, passenger estimates were rounded to the nearest whole integer.
Using a mean and standard deviation computed from observed data, a normal distribution for each TAZ OD pair, trip purpose, time of day bin, day type, and month was generated, from which a simulated number of passengers could be drawn. This normal distribution was then shifted based on the ridership return proportion dictated by the scenario, by multiplying the mean and standard deviation. Similarly, a normal distribution was used to describe the passenger type proportions observed for each TAZ OD pair, trip purpose, time of day bin, day type, and month – what proportion were ambulatory and what proportion were wheelchair users? These proportions were not adjusted in any way – it was assumed the proportion from 2019 would hold going forward. After applying these proportions, passenger estimates by type were rounded to the nearest whole passenger.
We now have both the trips we need to assign and the passengers that will be on board for each trip. Now we need to assign them to garages, vehicles and providers (HandyDART or Taxis).
2.4.2 Step 2: Assign Trips to Garages/Vehicles
As described in the assumptions, trip assignment to garages was simplified to assigning them either to a primary or secondary garage – this assignment is handled in the linear program discussed in a moment. The garage assignment groups were joined to the set of forecasted trips based on their origin TAZ. Trips were then rolled up to the day level – summed across time bins – so that vehicles could be assigned on a daily basis, as vehicle/driver shifts cross multiple time bins. In step 5 we will estimate how these are broken back out to time-of-day level estimates.
After assembling these demand estimates by garage assignment group and day, a linear program was specified which would assign passengers within garage assignment groups to a) garages and b) vehicle types within those garages. Linear programs are typically used in optimization processes (in transportation and other domains) where you are trying to maximize (or minimize) some outcome while meeting a set of constraints. In this case the objective function (the outcome you are trying to optimize) for the linear program was to maximize the number of passengers delivered across the HandyDART system in the model day – a separate linear program was constructed for each model day simulation. Built into the objective function that within each garage assignment group, passengers could only be assigned to vehicles at two garages. The constraints we had to meet with this objective function were the following:
- Each garage has a limit on the number of vehicles that can be assigned to it, and each garage has to maintain a 10% spare ratio. This means we can only assign 90% of the allowed vehicles at each garage.
- There is a limit on the total number of MICRO and MIDI vehicles available, and we also need to maintain a 10% spare ratio across the system (for each vehicle type). Therefore, we are limited to assigning 90% (each) of the total MICRO and MIDI vehicles available.
After running the linear program, the number of passengers not able to be served (if there were any unable to be served by the solution to the linear program) were then set aside to be allocated to taxis.
2.4.3 Step 3: Assign Cancellation to Trips
Similar to above processes, a normal distribution was generated for the rate of cancellation from the observed mean and standard deviation of the cancellation rates in 2019-2020, stratified by provider, month, day type. These distributions were used to select a random cancellation rate for each group of trips generated in the previous two steps. These cancellation rates were then multiplied by the generated trips to estimate delivered trips and canceled trips.
Trips were then separated by provider for the next few steps – only HandyDART trips proceeded through Step 4 and 5, and only taxi trips proceeded through Step 6.
2.4.4 Step 4: Estimate HandyDART Service Hour Needs (HandyDART only)
A primary desired outcome of the model was an estimate of HandyDART service hours delivered. The service hours needed to deliver a trip or a collection of trips depend on a variety of factors (e.g., distance, degree of trip overlap, time of day). Determining the precise balance of factors predictive of service hours needed would be a much more involved process than the model used hereien. Rather than understanding the underlying patterns determining service hour needs, we were interested in predicting service hours needed as accurately as possible for the simulated trips developed above. A black box machine learning algorithm – a random forest model – was trained upon all the observed existing data, so that the model could be used for prediction on unseen data (i.e. the data we developed in steps 1-3). The random forest model was trained on the following variables (called features in machine learning parlance):
- # of trips delivered
- # of trips canceled
- # of passengers delivered
- # of passengers canceled
- Vehicle type
- Number of vehicles
- social distancing requirement (i.e. 6’, 3’, or 0’)
These variables were selected by considering a variety of test models trained on a portion of the observed data (the training set) and then tested on the portion left out of the model (the training set). This model testing process is known as cross validation. Only variables that could be reproduced by the simulation in steps 1-3 were used, so that service hours could be predicted directly from the simulated data. This part of the overall model would be improved with more training data – i.e. data from 2018, as well as more observations from the post-COVID-19 period in late 2020 and early 2021.
2.4.5 Step 5: Distribute Total Estimated Daily HandyDART Service by Time of Day (HandyDART only)
The assignment of trips and service hours was done at the day level because driver shifts and trips obviously cross over multiple time bins. Nevertheless, understanding the time of day patterns is important for HandyDART’s resource allocations, especially pertaining to shift scheduling and peak vehicle needs. Therefore, the day level estimates were distributed back to the time of day level using the demand profile (by time of day) generated in step 1. This meant that trips and service hours were assigned proportionally to correlate with the demand distribution by time of day. The peak vehicle profile was assigned so that the peak vehicle need was assigned to the time of day with the peak demand. As with other steps, this was done for every simulation so that a variety of estimates are generated, which can then be turned into an average and/or confidence interval.
2.4.6 Step 6: Estimate Taxi Service Needs and Distributed by Time of Day (Taxi Only)
We do not know how many taxi service hours or unique vehicles are needed to serve taxi demand, but we do have in the data an record of the number of runs needed. We therefore generate this as a proxy for taxi service needs. Translink will need to evaluate – with the knowledge of local taxi vehicle/capacity limitations – whether the taxi runs generated are feasible to be served. The feasibility of a taxi solution was not evaluated, as taxis were where all excess demand was allocated. It is likely that in higher demand scenarios, some of these trips would ultimately be denied or delayed until another time where capacity was not as constrained.
Similar to the service hour model in Step 4, a taxi run model (also a random forest model) was trained on the observed taxi data. The taxi run ‘model’ was actually composed of two separate (but related) random forest models – one to predict the scheduled trip rate (as taxis serve a number of unscheduled trips per day), and one to predict the scheduled runs (based on both scheduled and unscheduled trips as estimated from the schedule rate model). The scheduled trip rate model was based on the following variables:
- # of trips delivered
- # of trips canceled
- Origin garage
- Day type (weekday/weekend)
- social distancing requirement (i.e. 6’, 3’, or 0’)
The scheduled run model was based on the following variables:
- # of trips scheduled
- # of trips unscheduled
- # of trips delivered
- # of trips canceled
- Origin garage
- Day type (weekday/weekend)
- social distancing requirement (i.e. 6’, 3’, or 0’)
As in step 4, variables were selected based on a variety of test models that were then cross validated to select the best performing model.
As with the HandyDART trips in Step 5, taxi trips and runs were distributed by time of day according to the simulated time of day demand profiles.
2.4.7 Step 7: Save out Model Results and Performance
Model results were then collected and saved out to the PostgreSQL database set up for the model, so that they could later be pulled for the results dashboard. Model performance statistics were also recorded.